SPSS-based ANOVA

Summary

Currently, there are four main methods used for ANOVA in SPSS: one-way ANOVA based on the "one-way ANOVA" procedure, one-way ANOVA based on the "univariate" procedure, two-way ANOVA without repeated observations based on SPSS software, and ANOVA with repeated data such as cross-grouping based on SPSS software.

Principle

The basic principle of one-way ANOVA using SPSS software is that when k (k ≥ 3) overall averages need to be compared, 1/2k (k-1) differences will be generated, and if these differences are to be tested one by one, the probability of committing a type Ⅰ error will be greatly increased with the increase of k, leading to an increase in experimental error and a decrease in the precision of the estimation. Therefore, it is not possible to apply t-test or u-test directly for hypothesis testing between two means. For this reason, statisticians have proposed a method to test for the presence of significant influences in a k ≥ 3 system, which is essentially a quantitative analysis of the causes of variation in the observations and is called an analysis of variance (ANOVA).

(1) Linear model and basic assumptions

Assume that a single-factor experiment has k treatments, each treatment has n repetitions, and there are a total of kn observations. The data structure of this kind of experimental data is shown in Table 5-1.

(2) Sum of Squares and Degrees of Freedom Profiles

In Table 5-1, the total variation of all observations is the sum of the squared deviations of the observations x from the total mean x, denoted as SSr, which is given as:

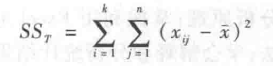
The decomposition is obtained:

② Segmentation of Total Degrees of Freedom In calculating the total sum of squares, each observation in the data is subject to the condition that "the sum of the outlying differences is 0", so the total degrees of freedom is equal to the total number of observations in the data minus 1, i.e., the total degree of freedom, _dfT = kn -1. The total degrees of freedom can be segmented into two parts: inter-treatment degrees of freedom, _dft = k -1, and intra-treatment degrees of freedom, _dfe = kn - k = k(n - 1). The sum of the squares of the components divided by their respective degrees of freedom yields the total mean square, the inter-treatment mean square and the intra-treatment mean square, denoted as _MST, _MSt and _MSe, respectively.

(3) F-distribution and F-test

In a normal population N (μ, σ2), k samples with sample content n are randomly selected, and the observed values of the samples are organized into the form of Table 5-1. Thus, both 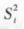and can be calculated as estimates of the error variance σ2 according to Eq. Find the ratio of as the denominator and as the numerator. Statistically, the ratio of two mean squares is called the F-value, i.e.:

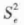
F has two degrees of freedom: _df1 = _dft = k - 1 and _df2 = _dfe = k(n-1). If a series of samples from this aggregate is continued for a given k and n, a series of F values are obtained. The probability distribution of these F-values is called the F-distribution. The critical values _F0.05 and _F0.01 can be found from the table of critical values for F.

The F-test is a method of inferring whether the variances of two aggregates are equal by the magnitude of the probability of the F-value occurring. In a one-way ANOVA, the null hypothesis is _H0: _μ1 = _μ2 = ..... = _μk, and the alternative hypothesis is _HA: the _μi are not all equal. If F ＜ _F0.05 ( _df1, _df2 ), i.e. P ＞ 0.05, accept _H0, indicating that the difference between treatments is not significant; if _F0.05 ( _df1, _df2 ) ≤ F ＜ _F0.01 ( _df1, _df2 ), i.e. P ≤ 0.05, negate _H0, accept _HA, indicating that the difference between treatments is significant; if F ≥ _F0.01 ( _df1, _df2 ), i.e. P ≤ 0.01 , negate _H0 and accept _HA, indicating that the differences among treatments are highly significant.

(4) Multiple comparisons

① Least significant difference method. The method of least significant difference (LSD) is the simplest method of multiple comparisons, and the steps of multiple comparisons using the LSD method are as follows: list the multiple comparisons of the mean table, and the treatments in the comparison table are arranged top-down according to their means from the largest to the smallest; calculate the least significant difference between _LSD0.05 and _LSD0.01; and compare the difference between the two means in the multiple comparison of means table with LSD0.05 and _LSD0.01. The difference between the two means in the table of multiple comparisons of means is compared with _LSD0.05 and _LSD0.01, and statistical inferences are made.
The scale formula for multiple comparisons of LSD method is:

② Duncan method The Duncan method considers the difference of the means as the extreme deviation of the means, and uses different test scales according to the number of treatments included in the range of the extreme deviation (known as the ordinal distance), k, in order to overcome the shortcomings of the LSD method. These different test scales depending on the rank distance k at the significant level α are also called the least significant extreme deviation LSR.
The formula is:

The basic principle of two-factor ANOVA is that when the trait under study is affected by two factors at the same time and two factors need to be analyzed at the same time, two-factor ANOVA can be performed. The relatively independent role of each factor is called the main effect of the factor (main effect); a factor in another factor at different levels of the effect of different, there is an interaction between the two factors, referred to as interactions (interaction). Interaction between factors is significant or not related to the utilization value of the main effect, if the interaction is not significant, then the effect of each factor can be added, the optimal level of each factor combined, that is, the optimal combination of treatments; if the interaction is significant, then the effect of each factor can not be directly added, the selection of the optimal treatment should be based on the direct performance of the combination of the treatment selected.

(1) Two-factor ANOVA without repeated observations

Unduplicated observations means that each treatment is not duplicated, i.e., assuming that there are a level of factor A and b levels of factor B, and there is only one observation for each treatment combination. The data structure of the unduplicated data is shown in Table 5-2.

The linear model for the observations in the two-way ANOVA is:

The results of the two-factor ANOVA with no replicated data can be summarized in the form of Table 5-3.

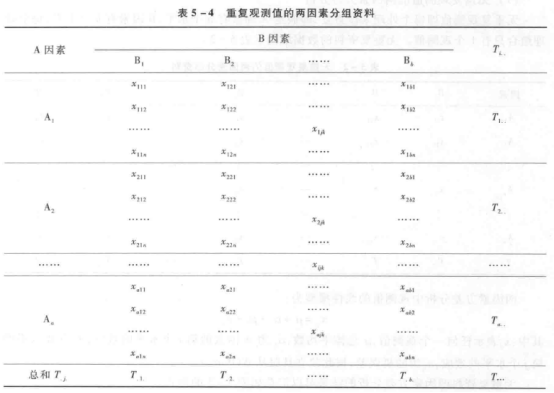
(2) Two-factor ANOVA with repeated observations

In a two-way ANOVA without repeated observations, the estimated error is actually the interaction of the two factors, and this result holds only if there is no interaction between the two factors, or if the interaction is small. However, if there is interaction between the two factors, the experimental design must be designed with repeated observations, which can estimate the interaction as well as the error at the same time. A typical design for a two-factor experiment with equal replicated observations is to design n replications for each combination of different factor levels, assuming that factor A has level a and factor B has level b. The data pattern is shown in Table 5-4.

The linear mathematical model for two-factor information with repeated observations is:

The results of the two-factor ANOVA for repeated observations can be summarized in the form of Table 5-5.

For more product details, please visit Aladdin Scientific website.

https://www.aladdinsci.com/